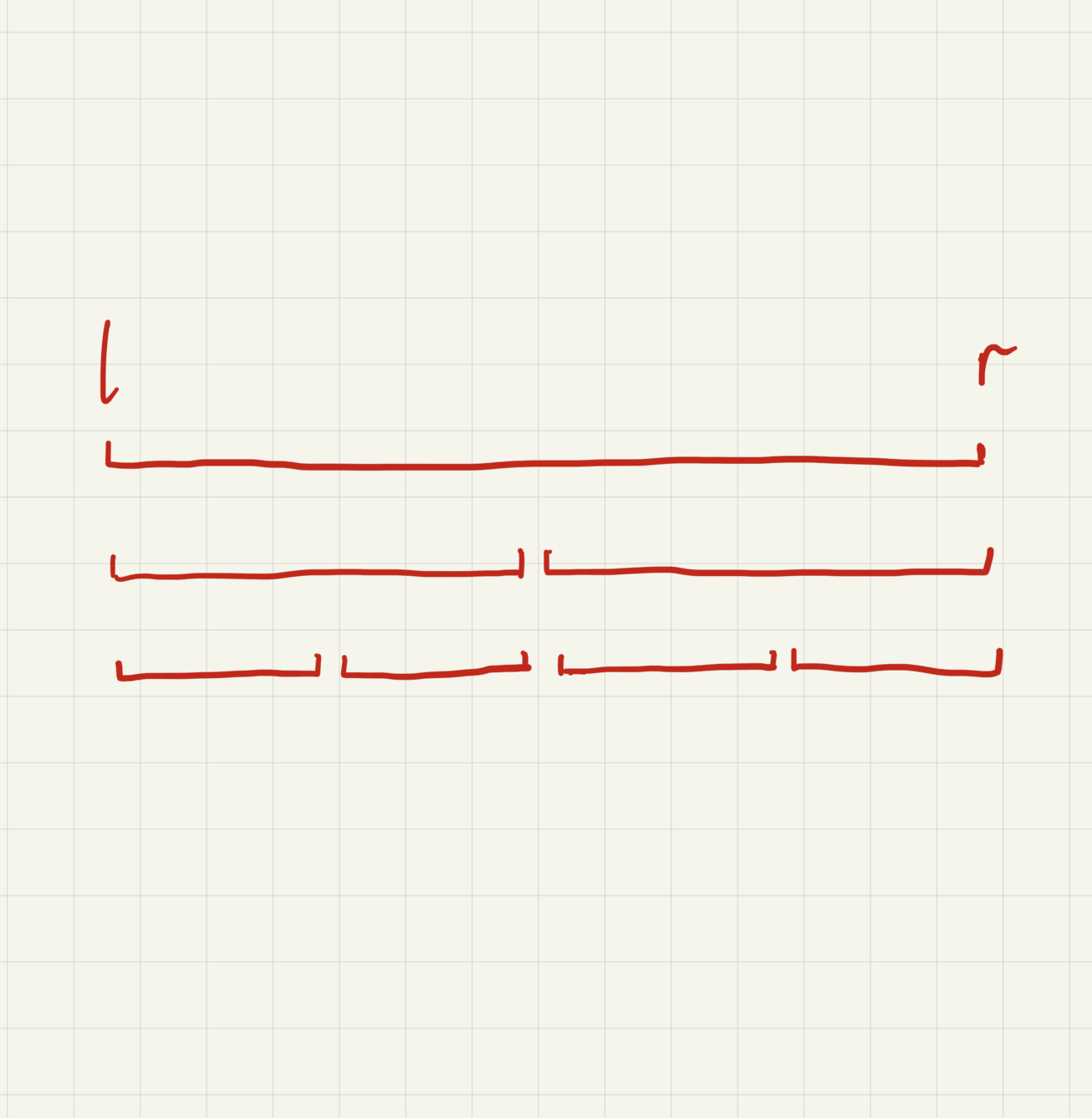
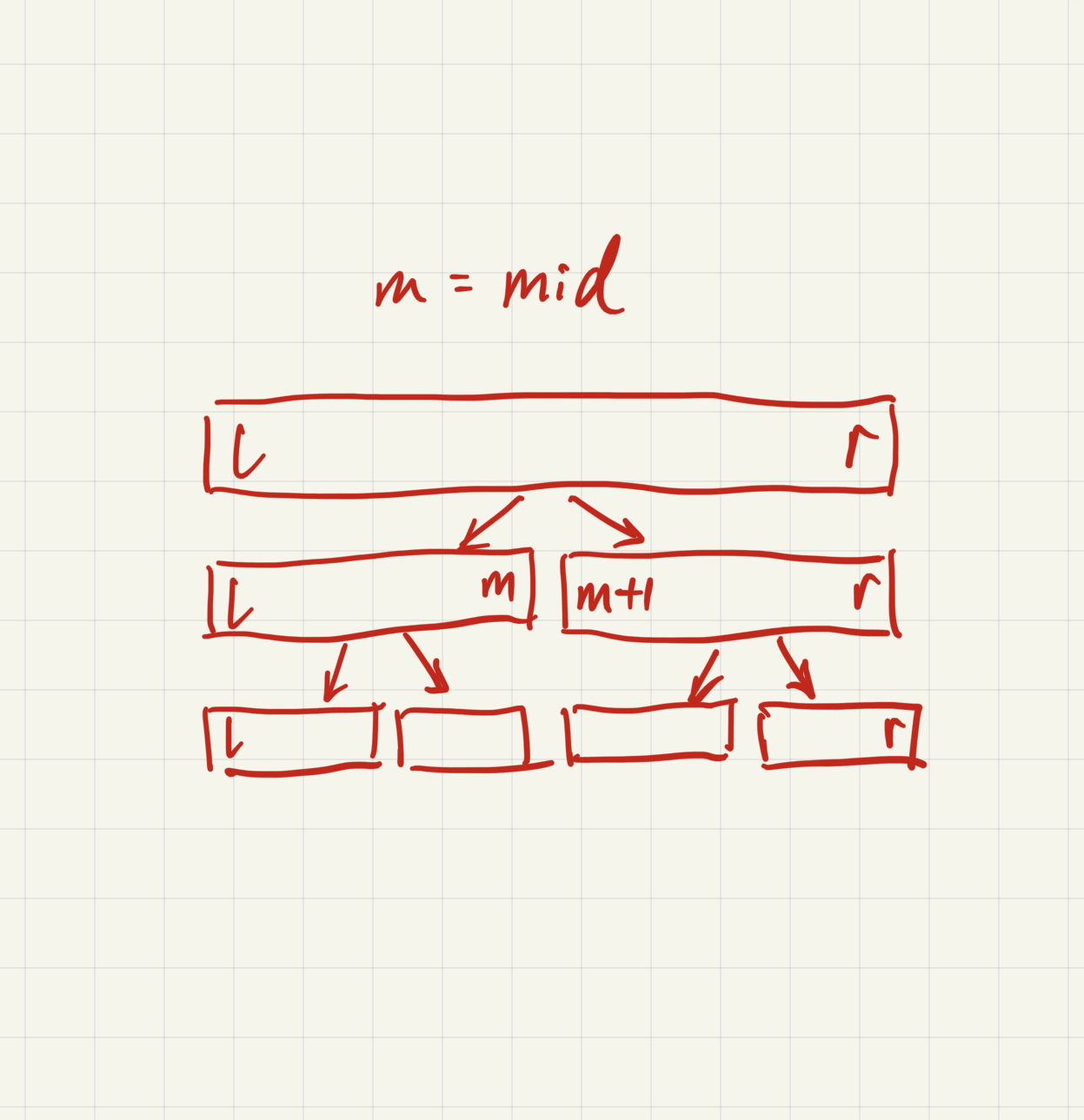
Data structure for storing information about intervals(very efficient btw).

DISCLAIMER:

I AM A TERRIBLE PROGRAMMER SO DO NOT TAKE THINGS I SAY SERIOUSLY. I KNOW ABUSOLUTELY NOTHING ABOUT WHAT I AM TALKING ABOUT. MY BLOG IS JUST A PLACE FOR ME TO REFLECT.

Definition

The segment tree, is a data structure used for storing information about intervals or segments. It allows efficient altering of interval’s or segments’s information, querying about information on intervals or segments. In this blog I will keep it to intervals, the only reason of this is I only learnt about the interval part. Given a interval, we can create a tree to store information about this interval, like my very accurate and clear sketches:

Building A Tree

To build a segment tree, we need to know what’s the interval we want. Say it’s [l, r]. We use recursion method to recursively build the tree. After building a node, we build two children of it, further dividing its interval, until new nodes have their l = r. You can have a separate initialize array for initial value for the nodes.

Combining Information

Well now we have a structure, what should we do with it? We want to extract information from it. This step requires the combining of informations because we need information to flow from leaf nodes to root node. In this blog we will take the classic sum as an example. Obviously, sum of the node is the sum of its children’s values.

Altering Information

We also want to manipulate the tree to store data. For example, we want to add k to all elements in [l1, r1]. If this is done solely using a array, you would have to go through l1 to r1. Not efficient. But imagine you have a node that satisfy l = l1, r = r1, you only have to add to that node. But do you go further down to its children and add to them as well? Well, no. But how’s that going to work? We use a ’lazy’ tag to cache additions. Confusing? Watch next part.

Lazy Tag

You are probably wondering, if I add to every node inside [l, r], that would be O(nlogn), where using an array is only O(n). That would be correct and the precise reason why we need the lazy tag. Suppose after some additions we want to query about certain intervals. If I added k1 to [l2, r2], and query was [l2, r2], does the children’s value really matter? No, because we don’t use them in any way. So maybe the addition to its children’s value is not necessary. Only if a query, say [l2, r2-1] is called do we need to process the information of node [l2, r2]. Until then, information is stored using the lazy tag.

Segment Tree Overview(Code)

#include <iostream>
using namespace std;

const int maxn = 100005;
//Segment Tree Node
struct Node{
	long long data;
	int l, r;
	long long lazy;
} t[maxn << 2];

//arr is the init array
long long arr[maxn];

//build the segment tree
void build(int p, int l, int r){
	t[p].l = l;
	t[p].r = r;
	t[p].lazy = 0;
	if(l == r){
		t[p].data = arr[l];
		return;
	}

	int mid = (l + r) >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
	t[p].data = t[p << 1].data + t[p << 1 | 1].data
}

//push down the lazy tag
void pushdown(int p){
    if(t[p].lazy == 0) return;
    t[p<<1].lazy += t[p].lazy;
    t[p<<1|1].lazy += t[p].lazy;
    t[p<<1].data += t[p].lazy * (t[p<<1].r - t[p<<1].l + 1);
    t[p<<1|1].data += t[p].lazy * (t[p<<1|1].r - t[p<<1|1].l + 1);
	t[p].lazy = 0;
}

void add_interval(int p, int l, int r, int k){
	if(l <= t[p].l && t[p].r <= r){
		t[p].data += k * (t[p].r - t[p].l + 1);
		t[p].lazy += k;
		return;
	}

	pushdown(p);
	int mid = (t[p].l + t[p].r) >> 1;
	if(l <= mid) add_interval(p << 1, l, r, k);
	if(r > mid) add_interval(p << 1 | 1, l, r, k);
	t[p].data = t[p << 1].data + t[p << 1 | 1].data;
}

long long query(int p, int l, int r){
	if(l <= t[p].l && t[p].r <= r) return t[p].data;
	pushdown(p);
	int mid = (t[p].l + t[p].r) >> 1;
	long long ans = 0;
	if(l <= mid) ans += query(p << 1, l, r);
	if(r > mid) ans += query(p << 1 | 1, l, r);
	return ans;
}

WalkThrough

Build Function

const int maxn = 100005;
//Segment Tree Node
struct Node{
	long long data;
	int l, r;
	long long lazy;
} t[maxn << 2];

//arr is the init array
long long arr[maxn];

//build the segment tree
void build(int p, int l, int r){
	t[p].l = l;
	t[p].r = r;
	t[p].lazy = 0;
	if(l == r){
		t[p].data = arr[l];
		return;
	}

	int mid = (l + r) >> 1;
	build(p << 1, l, mid);
	build(p << 1 | 1, mid + 1, r);
	t[p].data = t[p << 1].data + t[p << 1 | 1].data
}

Here, p«1 is p2, p«1|1 is p2+1. Using this allow us to have 1->2,3; 2->4,5; 3->6,7; See the pattern here? The last line of code is actually the ‘push up’ function, but since this is such a basic example, a additional pushup function is unnecessary(pushup function combines the information from the children and push it to the parent). Build() builds the tree recursively, each time initializing a node and go deeper into the tree.

Pushdown Function

//push down the lazy tag
void pushdown(int p){
    if(t[p].lazy == 0) return;
    t[p<<1].lazy += t[p].lazy;
    t[p<<1|1].lazy += t[p].lazy;
    t[p<<1].data += t[p].lazy * (t[p<<1].r - t[p<<1].l + 1);
    t[p<<1|1].data += t[p].lazy * (t[p<<1|1].r - t[p<<1|1].l + 1);
	t[p].lazy = 0;
}

This part is called the pushdown function. As the name suggests, it pushes the data from the parent to two of its children. It’s worth noting that when we call pushdown() on a node, only the next layer of children are getting updated. If all children starting here get updated, it wouldn’t be much of a lazy tag, the job is just done. The children are now up-to-date, and the cache is moved to the children. If we don’t need to go deeper, this can satisfy us on these children’s level. If we wish to go further, we need to call pushdown() on these children. In other words, we will not update any node unless we are forced to. We are, well, lazy.

Adding To Entire Interval

void add_interval(int p, int l, int r, int k){
	if(l <= t[p].l && t[p].r <= r){
		t[p].data += k * (t[p].r - t[p].l + 1);
		t[p].lazy += k;
		return;
	}

	pushdown(p);
	int mid = (t[p].l + t[p].r) >> 1;
	if(l <= mid) add_interval(p << 1, l, r, k);
	if(r > mid) add_interval(p << 1 | 1, l, r, k);
	t[p].data = t[p << 1].data + t[p << 1 | 1].data;
}

This function adds k to all element in [l, r]. The way we achieve this is as follows: If current node’s interval is completely inside [l, r], we just need to add to this node, and cache the change in lazy. If current node’s interval isn’t completely inside [l, r], we divide [l, r] into [l, mid] and [mid+1, r] where mid is the mid of current node’s mid, and pass it down. What will happen is that eventually the further divided interval will encounter a node with the exact boundaries, and gets taken into lazytag.

The pushdown() is called before making any changes to ensure from root node to current node, everything has been updated correctly.

Querying

long long query(int p, int l, int r){
	if(l <= t[p].l && t[p].r <= r) return t[p].data;
	pushdown(p);
	int mid = (t[p].l + t[p].r) >> 1;
	long long ans = 0;
	if(l <= mid) ans += query(p << 1, l, r);
	if(r > mid) ans += query(p << 1 | 1, l, r);
	return ans;
}

This function returns sum of all element from l to r. The way it achieves just that is as follows: If current node’s interval is completely inside [l, r], we just need return the value of this node. If current node’s interval isn’t completely inside [l, r], we divide [l, r] into [l, mid] and [mid+1, r] where mid is the mid of current node’s mid, and pass it down. What will happen is that the value will return, starting from the closest node to root node possible that is inside [l, r], preventing it going further down therefore reduce time complexity.

Usage Example

int n = 30;
build(1, 1, n);
add_interval(1, 2, 7, 9);
cout << query(1, 3, 6);